Do executable semantic models need a syntax?
A case against standards in software composition and data exchanges
|
Author: |
Armin Rigo |
|
Date: |
24 sep - 11 oct 2003 |
1 - Abstract
This draft recalls a variant of a classic model, a cross between category theory and ontology models of data representation and execution, and proceeds to suggest how the model could be used as a basis for actual execution without having to agree on a standard formal syntax to express the model in.
More generally it is a case against standards in the computer research and industry, defending the point of view that they are unnecessary and counter-productive for software composition, interoperability, and data exchange formats and protocols.
2 - Models of concepts
2.1 - Introduction
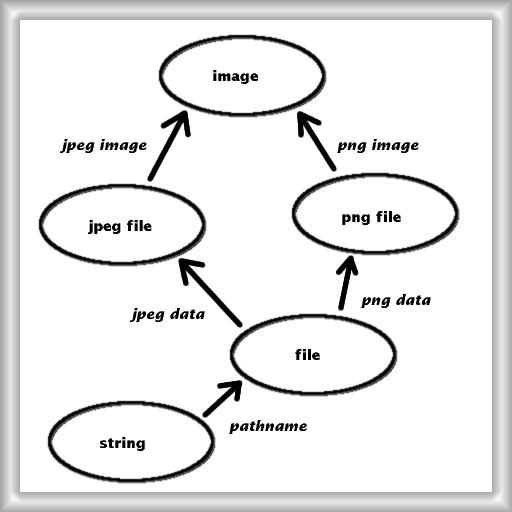
figure 1 - the Basic Images model
The models we will use in the following consist of two building blocks:
-
concepts, a term by which we mean more precisely a concept that has been identified and reified into the model. They are the circles in the above picture.
-
functors that capture a relationship between two concepts, represented as arrows above. A functor is more precisely some way to see some instances of a concept as instances of another concept.
We call model a graph of functors linking concepts; the above picture represents a model. The five concepts and five functors it depicts should have a clear meaning: they show how a string of characters can be thought of as the path to an image file in two different ways, via the two different paths that we can follow from string to image.
Philosophically, we take the point of view that concepts are intentional; they are not identified with their extension, the set of all instances of the concept. The latter is a category. However, in general we will neither talk about extension nor individual instances at all, on the rationale that a "physical object" as we may think about it can never be fully formalized in any system. As far as a computer is concerned, an "object" in the head of the programmer is always an ideal that can only be approximated by some a set of properties.
Being intentional, no functor or concept can be fully described in any formal language. In particular, we will not attempt to formalize interfaces to operate on the objects. This is in contrast with the object-oriented (OO) paradigm, in which a single formalism, usually that of class, is used to capture both (implicitely) the intension of the objects and (explicitely) an interface through which they can be manipulated. In our model a concept only expresses the intension. The same holds for the functors, which are thus more flexible than the OO notion of inheritance. In the above diagram it would not make sense to think about image as a base class of string, if only because of the two different paths with different meanings.
The important, easily formalizable point is the graph formed by functors and concepts.
2.2 - Model-driven execution
Here is a quick overview showing how a model can be executed without formalizing the concepts and functors.
In a given programming languages, some of the concepts captured by concepts and functors can be readily identified with some core features provided by the language. This is the case, for example, of string and file in the Basic Images model of figure 1, and of the pathname functor -- the latter is implemented by the function that opens a file given its name, say open(filename). The other concepts could also be identified, e.g. as subclasses of a newly designed Image class, but we will leave them as abstract for now.
The goal of the model is to allow the discovery of possible connexions between existing algorithms and tools. Assume that we have a procedure or method to display a JPeg file, say show(f) taking a file object f as argument. Suppose moreover that we have a function encode_jpg(src, dst) that decodes a Png image given by file called src and encodes the result as the JPeg file named by dst. Clearly, it should be possible to compose them to display a Png file; the point is that it should be possible to figure out the correct composition automatically.
The search operation itself can be performed by an inference engine; for now let us assume that such a tool is available. The problem left is to express the necessary information. We will do so, first informally then a bit more precisely, by completing the identification of concepts that we started above for the programming language's core features. Obviously, from the programming language's point of view, show is a function whose single argument lives in its understanding of the file concept, and encode_jpg takes two string arguments. This is how much a classic, static type system can tell you. But if we proceed naively, then if we start with a string object (the name of a Png file) and want to display it, we can expect an inference engine to figure out that the most direct way to do so is to turn the string into a file object via open and then call show. This is wrong; encode_jpg should have been called at some point. Moreover, there might be other ways to turn a string into a file (e.g. saving the string into a temporary file); how should the engine know which one to use? In other words, what information does the engine miss that seems so obvious to us that we find the correct answer in a nutshell?
The problem is in the identification of the concepts. The function show cannot display an arbitrary file; it can only work specifically those files that adhere to the JPeg standard. And the given string is not just a string of characters, we know that it is the name of a Png file. Expressing these facts is what we must do next.
So the input string lives in string but is really meant to be a png_file via the composition of the pathname and png_data functors; we could say that it is a png_file implemented as a string via the given functor composition. Similarily, show takes an argument which is a jpeg_file which must be implemented as a file.
Now we need to introduce encode_jpg: it is the string * string implementation of a png_file * jpeg_file function, where * denotes pairs; the first string is related to png_file via the composiion of pathname and png_data, and similarilty for the second string.
There is still no way the engine could figure out that it should automatically use encode_jpg. What is so special about this function? Should it be somehow tagged as a conversion function, so that the engine knows that it can use it transparently whenever it needs to? This approach is common in object-oriented typed languages, but we strongly feel that it is inadequate. There are certainly situations in which we do not want automatic conversion to take place under our feet. For example, the JPeg file format is lossy, which is inacceptable for some applications -- a fact that was not expressed in the model, because it is perfectly fine in our case and we do not want to have to consider it.
Note that we did not use yet the upper part of figure 1 -- the image concept. The distinguishing feature of encode_jpg is that the result is the same image as the original, at least if we think about an image as a (possibly approximate) visual impression and not an array of pixels with precise numeric values. This last distinction shows that, a posteriori, we have made the image concept a bit better-defined by explicitely not requiring exactness. Still, this is fine, because we never said that an image must conform to any specific array-like interface.
Thus, some ontologies come equipped with an equality. For image it is the non-formalizable idea of looking the same. Instead of introducting a separate notion, a nicer way to think about equality will be shown later (figure 2). For now, consider the equality as a relation of two image arguments, i.e. say that eq_image(X,Y) is true if and only if X and Y are the same image. Map png_file * jpeg_file to image * image via respectively png_image and jpeg_image. Then we express that encode_jpg is the same as eq_image via this correspondance.
If we had previously seen the encode_jpg on png_file * jpeg_file to be the interface of the function, and the one on string * string to be its implementation, then we could come up with a hefty word like "intensional interface" to designate eq_image. We prefer to see "interface" and "implementation" as an arbitrary duality between only two levels of abstraction -- there can be any number of them.
A last point must be fixed to make the model wholly executable: the purpose of show is in fact not to display a jpeg_file, but an image -- the given implementation works on a file which is seen as an image through the composition, specifically, of jpeg_data and jpeg_image.
Pseudo-code summary (with open expressed as equality too):
the language function show(file) maps to:
show( jpeg_image( jpeg_data( file ) ) ).
the language function encode_jpg(src, dst) maps to:
eq_image( png_image( png_data( pathname( src ) ) ),
jpeg_image( jpeg_data( pathname( dst ) ) ) ).
the language variable X (the name of the file to display) maps to:
png_image( png_data( pathname( X ) ) ).
the language function call file=open(name) maps to:
eq_file( file, pathname( name ) ).
Note again that we never formalized the involved ontologies; they have no counterpart in the concrete programming language. The inference engine can figure out with only the above declarations that when we say show(X) we mean the following sequence of concrete calls:
encode_jpg(X, J) F = open(J) show(F)
This is found by searching which applications of which equalities are needed to transform show(png_image(png_data(pathname(X)))) into the only declaration available for show, and deduce the corresponding sequence of concrete calls.
2.3 - The generalization process
This simple example already shows that the specification may be relatively complicated to get right. There are "obvious" things that we do intuitively which must be expressed.
However, the initial impression that carefully-planned OO-style design is needed is deceptive. The process we followed is incremental: the model we started with need not be complete. Typically, there is no need to introduce the image concept before we actually see a need for it.
It was not immediately obvious that the show operation was actually defined on image instead of on just jpeg file. It is thus an important part of the generalization process that we should be able to declare that, a posteriori, a given algorithm actually applies to a broader class of objects, or equivalently turns out to depend less on details than was initially foreseen. (Not that we have seen a reason to prevent it or even that special support should be needed for that; at this point we are merely investigating the aspects and consequences of the model.)
It is thus possible to build incrementally a large graph by extending it both upwards and downwards, switching as needed between levels of abstraction. In this approach, an essential way to extend a graph is upwards, i.e. by generalization. No special techniques are needed. Contrast this with the difficulties of generalization encountered in many more formal approaches. Most OO languages do not allow -- or require special features for -- adding new base classes to existing classes. In the most flexible knowledge-based systems, problem-solving methods are described as a basic general method on which a tower of specializers is added. In both case the focus is from general to specific, though it is generally admitted that the engineering of concepts typically starts from specific examples and grows in generality as much as, and not more than, needed in the particular application.
2.4 - Equality
The equality of objects is a perfect example of concept that we reached by generalization but turns out to be important on its own. We can extend the original model to include explicitely a concept of object that come with an operation of equality:
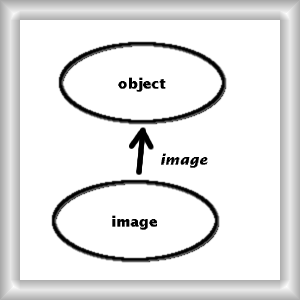
figure 2 - the Equality for Images
We would then express that eq_image corresponds to the abstract eq via the given functor. In doing so, we have shifted the point of view: we not longer consider equality as an intrinsic characteristic of a concept. It is now relative to a functor. It is the functor which specifies how instances of the concept should be regarded as equal. In this point of view, we can (if we wish) unify concepts which differ only in how their instances are to be distinguished, like fuzzy image and exact image. We would simply have two different functors from this now unique concept to the object concept.
Note how this point of view generalizes the existence of different equalities in most programming languages. Equality-by-value is not equality-by-identity. Common Lisp has got four of them in stock (eq, eql, equal, equalp)! Few languages effectively allow the programmer to define more than one custom notion of equality (if at all) on a single concept. The powerful ML module system is an exception; it is a example that we will invoke again in the sequel.
Note that equality has still got a particularity in our model: a specific meaning to inference engine, that of substitutability. The engine must thus special-case this concept. We will come back to this below, when the engine is put back to where it belongs instead of being a detached entity.
An objection that can be drawn at that point against the above point of view is the burdens of having to specify all the time which particular functors we mean to use, instead of just talking about the concepts themselves. It may be foreseen that as the models grow there will be less and less room for "default" or "implicit" functors between any two concepts. However, we uncompromizingly adhere in this respect to the modern scientific idea that the only essential feature of any object of any domain is which relations it shares with other objects. An isolated object is meaningless. Similarily, we did not talk about the structure or formalization of concepts; they are completely meaningless until functors link them to other concepts. A concept like image is full of sense for a human being because he has related the concept to many others long ago. If formalized in a specific programming language, it is implicitely related to the syntax and semantics of the particular language (we even say defined by in this case). Alone in a model, it is just incomprehensible and useless.
An exemple of this is given in figure 2: there is no better name for the functor that sees an image as an object as, well, image. We expect that it will be common to identify a concept with a functor that relates it to an extremely abstract one like object. Even more extremely, for uniformity we may add (from category theory) a terminal concept (something) that all other concepts uniquely map to. Although we will not pursue this path further in the sequel, it means that we could theoretically never name the individual concepts but only the functors.
2.5 - Subjective models
Let us now try to develop larger concept models than the one exposed above. For example, consider the concept of list. We can express it easily, in a flavour similar to the list of dynamic languages, i.e. as a list of arbitrary objects. Alternatively, we could instead express a more specific concept, like that of list of integers. But with the tools we have so far we cannot express parametric concepts, e.g. list whose elements are instances of the concept T, for variable T.
Instead of introducing parametrization and the complex construction techniques it requires, we prefer the idea of introducing points of view. The whole world cannot be a single concept model anyway; different users and machines have different concept models. In a subjective programming vein, we will limit ourselves to small models that only contain as much concepts as needed for a specific task. What we will then need is a way to relate concepts between different models.
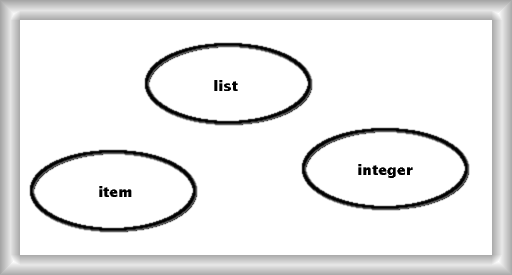
figure 3 - the List model
From a list's point of view, all it needs is the three concepts depicted in figure 3. The elements contained in the list are captured by the concept item. We can then define list operations using integers for indexing. The model of figure 3 is a bit boring because it uses no functor at all.
Suppose now that we want to use lists in other parts of the program. To do so, we import the List model into other models. In this respect models are very similar to the ML modules. Arguably, the point of view differs because the ML modules and functors are considered to be advanced typing features of the language, while we are trying to put models and concepts at the core of the execution model. Moreover, the correspondence between the concept of the original List model and their versions imported in another model is not necessarily direct. If, say, we want to talk about the concept of list of images, then we need our own, slightly different point of view on lists: what used to be item in the List model is now image in our model. The item concept could be called a parametric type because we expect it to correspond to different concepts in practice; we find it more useful to avoid talking about parametrization altogether because any concept in any model can be used in this way. In fact, one could argue that it is the only meaningful way to use a model anyway: to relate its concepts to concepts inside other models.
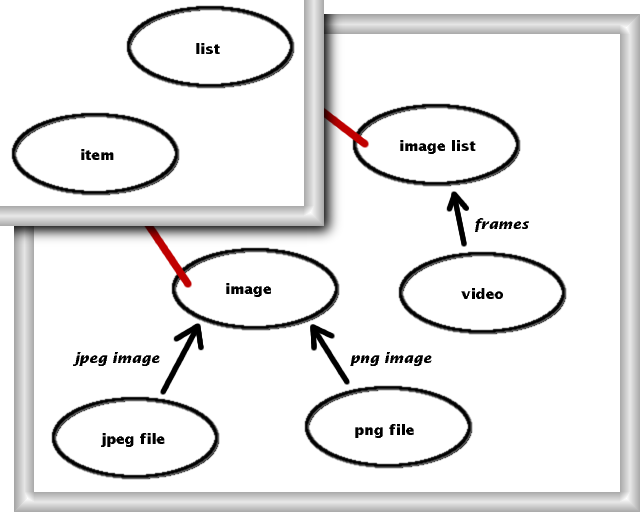
figure 4 - videos as lists of images
In figure 4 we relate the concept of video to the more abstract concept of image list via a functor, and then we express that the latter is exactly a list of images via inter-model identifications (in red). Note that a video is a priori more than just a list of images, thus the extra level of abstraction. A more complete approach would enforce imported concepts to always be at a higher level of abstraction than what we actually want to use it for in the model, or equivalently to consider the red links of picture 4 as another kind of functors. In this way we can dissociate the original concept from what the importing model thinks these concepts are. This is especially important in the presence of generalization, because all models importing the same concept may make different implicit assumptions about it.
Also note that there is no reason that a concept from a model should correspond to at most one concept in another model. We can use lists for different purposes in the same model.
The inter-model identification also imports the operations that were defined in the original model, so that in figure 4 we can talk about the operation of getting the nth element out of an image list, and provide a concrete implementation for it that would, say, return a jpeg file instead of only an image.
We believe that this procedure of defining a concrete operation as the implementation of an abstract one is a key point. Syntax-rich dynamic languages have proven to be extremely useful to express algorithms in a generic fashion when the abstract operations needed are precisely those defined by the syntax. For example, an number of languages have an operator x[y] whose intended meaning is to somehow index into a container object; algorithms written using this operator are directly reusable for any kind of container because of the consensus about what the operator should mean. Operations with no direct equivalent in the syntax (nor in standard libraries) force programmers to invent their own method names, and the resulting algorithms need much more documentation and boilerplate to be reused. We think that the procedure described above is a way to define and reuse operations without being limited by the syntax. Moreover, the ability to relate concepts and operations a posteriori (and let the inference engine deduce what it can do given these relations) avoids the standardization problem and turns it into an expressivity problem. Two independent concepts rarely turn out to be exactly the same; we must thus have ways to state in what respect the concepts are similar. This requires at least the ability to express which one generalizes the other one, or if a third one generalizing both can be found, or if the correspondance is still less direct how some operations involving one concept can be turned into operations involving the other one.
3 - Networks of models
3.1 - Formalization of models
So far we have been quite imprecise about how we plan to formalize concept models and operations. Drawing pictures only takes you so far in expressing concepts, and drawings are not executable.
The purpose of the present paper is not to introduce a programming language, even less to push forward an existing or new to-be-standard formalism. Instead, in coherence with the ideas developed above, we emphasis on the possibility for several formalisms to coexist. A concept model can thus itself be described in any language, provided there is a way either to execute it in that language or (better) to relate it to other languages. In other words, the models and the operations that we can apply to them could themselves be captured in the same framework of concept models.
To make this clear, let us consider the specific issue of operations. In different programming languages and styles, the very concept of operation has different meanings. In traditional imperative languages it is a statement or expression, say a procedure or function call. In functional languages it could be more specific, e.g. a pure function call with no side effects. In logic languages, on the other hand, it is more natural to use predicates instead of functions. All these ways of doing operations are different, but can be mapped to each other, more or less easily and more or less canonically.
It is possible, in any given language, to design simple structures in which we can write concept models as informally described above -- e.g. a set of classes, or term-manipulating predicates. An operation is formalized in whatever way is more natural in the given programming language.
3.2 - Model networks
A situation as described above will obviously lead to a number of different formalisms in different programming languages, and probably even various formalisms for the same language. We thus need a way to relate them to each other. There are essentially two different ways to do it. We can write ad-hoc translator utilities between some pairs of formalisms; or we can design a standard or meta-standard to which each individual formalism must relate. In practice the latter usually emerges from the former case, as one of the only ways to achieve some degree of transparent interoperability, although it is theoretically much less flexible than a "network" of ad-hoc translators -- in effect, it reduces each of these possibly different formalisms to a lowest common denominator, a library-style interface to an external component.
Let us concentrate on the reasons behind the failure of the "network" scheme. To link, say, a formalism in an OOP language A (a set of classes) and one in language B, we can enhance the classes in A so that they include methods to read and/or write data in some format natively understood by B, or use some communication protocol that we have implement both in A and B. This approach is ad-hoc in the sense that for each pair of formalism the programmer must be aware of the existing interfaces and invoke them explicitly, and often write yet other ones. (Clearly, and most importantly, the problem is continuously apparent to the user as well, who has to deal on a day-by-day basis with for him obscure incompatibilities in file formats, protocols, user interfaces, and so on.)
The above problem is precisely what the first part of the present paper was about: how concept models might help building and running a "network" of links between different concepts, given implementations for these concepts at various abstraction levels. It should then come as no surprise that we suggest that concept models are appropriate to describe the relationships between different formalisms used to implement the very concept of concept model. Therefore, we propose that the operations in a language A that translate between the formalism defined in A and the one defined in B be themselves annotated, as we did with images, as operations between concepts in a model of models -- which is itself described in A.
Given a powerful inference engine, say written in A as well, it is then possible to handle entirely automatically operations that were originally described in B only. The details of this operation are by no mean straightforward, and it is expected that such an inference engine will be a major piece of software. It should be able to choose between different possible implementation strategies, e.g. how much data must actually be transmitted to B for execution, or if on the other hand some operations defined in B can be entirely translated and executed in A. These issues are related to a number of research areas, e.g. distributed networks and persistence. It certainly requires help and hints from the programmer or even the end user to guide it in its choices. Such behavior, however, does not require a "complete artificial intelligence" -- an overview of what could be its underlying basic steps was given in the first part of the present paper. This could led to a situation essentially better than the current one, in which the user always has to know (from some external source) the existence of specific tools to take him from point A to point B.
3.3 - Reflective inference engines
We introduced reflectivity by formalizing networks of concept models as models themselves. Accordingly, the next step is to call meta-model a model whose concepts are again models. Note that we will also consider that no language has any privileged "built-in" structure to formalize models in (actually, to some extent, what really needs to be "primitive" in languages remain to be explored). Thus, meta-model must not be confused for a formal term: it is a model on which we have implied some kind of externally imposed idea about what the concepts are intuitively supposed to mean.
We can now consider the execution itself as an operation (in the formal sense) in such a meta-model. Once written, an inference engine, possibly decomposed in simpler operations, can be expressed in a meta-model inside of the very formalism that it operates on.
As in every other case throughout the present paper, expressing a complex inference engine in a concept model is optional, and doesn't save us the trouble from writing it in the first place; but doing so becomes useful when the operations in question must be composed in non-trivial ways. For an inference engine operating on models, it is useful when the system has several ways to represent the notion of model, which is exactly the situation described above. This allows a much more incremental and distributed construction of what we called the inference engine. Even a monolithic inference engine in a language A could theoretically send parts of itself (reflectively) to a language B; but the most interesting point is that inference can become a distributed operation as well, by allowing programmers to provide not only operations, and not only static declarations about them in some concept models, but also meta-operations, i.e. strategies on how to best compose operations. For simple cases, providing hints like expected resource costs for single operations might be enough for an inference engine to make reasonable choices, but clearly no hint language can be a priori expressive enough for all the cases in which the programmer appreciates finer control.
Naturally, these meta-operations are defined as usual operations in meta-models, at the appropriate abstraction levels (i.e. some meta-operations might be pretty general, while others only apply in specific cases). A family of the most general of these operations, possibly coming from various sources, can appear as a consolidated inference engine.
4 - Closing remarks
The present paper's aim is to describe the author's opinion about a useful system. The paper itself is work in progress. No experimental implementation exists yet, so take this all with a grain of salt if you didn't already!
Search for related work is in progress. Some would say Semantic Web here, but we put the Semantic Web into the "meta-standard" classification of model networks we sketched above. Our work is closer in spirit to the previous work in the Artificial Intelligence field focusing on ontologies, tasks and problem-solving methods, as described e.g. in Ontology-Oriented Design and Programming. A distinction is that we explicitely rule out having a single specific formal syntax, and rely instead on meta-level reflection.
Armin Rigo